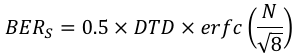RMS to Eye-closure Jitter Calculator

Assuming only random noise, you've quantified the time-interval error (TIE) jitter in a signal as an RMS value. You want to determine, if a bit-error ratio (BER) bathtub plot were to be measured for this signal, what the plot's eye closure is at a specified BER (that is, BER_S).

Note that TIE is the short-term variation of a digital signal's significant instants from their ideal positions in time, where a "significant instant" refers to the time a rising or falling edge crosses a threshold voltage (V_t).

The figure below illustrates one unit interval (UI), which is the duration of one bit in a data signal. The location of each edge in the signal is randomly distributed with a standard deviation of σ. Note that since the distribution's mean is zero, its RMS value equals σ.

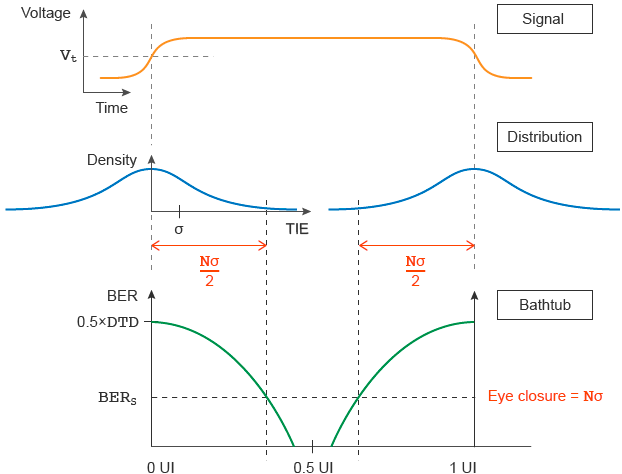
The eye closure is computed as Nσ, where N is a crest factor determining how much of the distribution's tail needs to be included for the BER to equal BER_S. The calculator computes this eye closure after solving the following equation for N,

where DTD is the signal's data-transition density. For data signals, DTD is defined as the ratio of transitions (or, edges) to the number of bits. For clock signals, set DTD=1.

Enter numbers below using integers or scientific notation (for example, enter 123 as 123, 1.23e2, or 1.23E2).

RMS to Eye-closure Calculator

The following table is provided for quick reference.