RMS-zu-Peak-Peak-Jitter-Rechner | Zurück zu Entwicklungsrechnern
Sie arbeiten mit einem Signal, das nur zufälliges Rauschen enthält, und Sie kennen seinen Jitter-Wert in Sekunden RMS. Für diesen Rechner ist der anwendbare Jittertyp für Datensignale der Zeitintervallfehler (TIE). Für Taktsignale kann der anwendbare Jitter-Typ beliebig sein (TIE, Perioden-Jitter, Zyklus-zu-Zyklus-Jitter usw.). Wenn die Jitter-Verteilung eine Gaußsche Verteilung ist, ist sie in jedem Fall durch eine Standardabweichung σ gekennzeichnet, wie unten gezeigt.
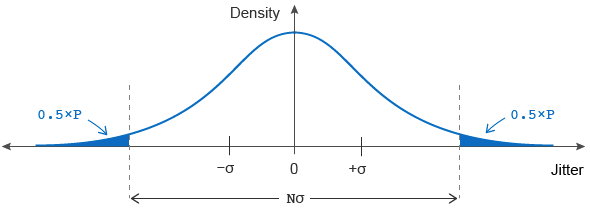
Beachten Sie, dass der RMS-Wert der Verteilung gleich σ ist, da der Mittelwert der Verteilung Null ist. Die Höhe der Verteilung hängt von der Wahrscheinlichkeit ab, dass das Signal so viel Jitter aufweist.
Ihre Anwendung wurde so konzipiert, dass sie ein gewisses Maß an Zuverlässigkeit aufweist. Daraus lässt sich ein akzeptabler Grenzwert für die Wahrscheinlichkeit P ableiten, dass das System ausfallen kann, wenn der Jitter zu groß wird. Grafisch entspricht diese Wahrscheinlichkeit der einfarbigen Fläche in der Abbildung oben als Prozentsatz der Gesamtfläche der Verteilung. Beispielsweise läuft ein Six-Sigma-Design (z. B. σ=±3) in 99,73 % der Fälle fehlerfrei (also P=0,0027, was einer durchschnittlichen Ausfallrate von 0,27 % entspricht).
Sie möchten wissen, wie groß der Peak-Peak-Wert des Jitters für diese Fehlerwahrscheinlichkeit P ist
Der Spitze-Spitze-Wert wird als Nσ berechnet, wobei N ein Scheitelfaktor ist, der bestimmt, wie viel vom Gaußschen Ende einbezogen werden muss, um die Fehlerwahrscheinlichkeit P zu erzeugen. Der Rechner berechnet diesen Spitze-Spitze-Wert, nachdem er die folgende Gleichung nach N gelöst hat ,
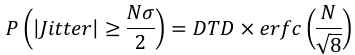
Dabei ist DTD die Datenübergangsdichte des Signals und erfc die komplementäre Fehlerfunktion. Für Datensignale ist DTD als das Verhältnis von Übergängen (oder Kanten) zur Anzahl von Bits definiert. Für Taktsignale setzen Sie DTD=1.
Geben Sie unten Zahlen in Ganzzahlen oder in wissenschaftlicher Schreibweise ein (geben Sie beispielsweise 123 als 123, 1.23e2 oder 1.23E2 ein).
RMS-zu-Peak-Peak-Jitter-Rechner
Die folgende Tabelle dient als Kurzreferenz.
| Wahrscheinlichkeit (P) | Crest-Faktor (N) | |
| DTD = 0,5 | DTD = 1 | |
| 1e-1 | 2.563 | 3.290 |
| 1e-2 | 4.653 | 5.152 |
| 1e-3 | 6.180 | 6.581 |
| 1e-4 | 7.438 | 7.781 |
| 1e-5 | 8.530 | 8.834 |
| 1e-6 | 9.507 | 9.783 |
| 1e-7 | 10.399 | 10.653 |
| 1e-8 | 11.224 | 11.461 |
| 1e-9 | 11.996 | 12.219 |
| 1e-10 | 12.723 | 12.934 |
| 1e-11 | 13.412 | 13.613 |
| 1e-12 | 14.069 | 14.261 |
| 1e-13 | 14.698 | 14.882 |
| 1e-14 | 15.301 | 15.479 |
| 1e-15 | 15.883 | 16.054 |
| 1e-16 | 16.444 | 16.610 |