RMS 到峰峰值抖动计算器 | 返回发展计算器
您正在处理仅包含随机噪声的信号,并且您知道其抖动值(以秒 RMS 为单位)。对于此计算器,数据信号适用的抖动类型是时间间隔误差 (TIE)。对于时钟信号,适用的抖动类型可以是任何类型(TIE、周期抖动、周期抖动等)。无论如何,如果抖动分布是高斯分布,则其特征在于标准偏差 σ,如下所示。
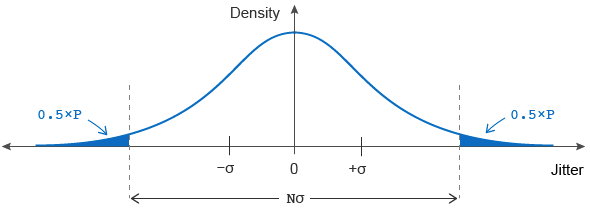
请注意,由于分布的均值为零,因此其 RMS 值等于 σ。分布的高度与信号具有如此大的抖动的概率有关。
您的应用程序被设计为具有一定程度的可靠性。由此,您可以得出当抖动太大时系统可能发生故障的概率 P 的可接受限制。从图形上看,该概率等于上图中的纯色面积占分布总面积的百分比。例如,六西格玛设计(例如 σ=±3)在 99.73% 的时间内运行无错误(因此 P=0.0027,表示平均故障率为 0.27%)。
您想知道该误差概率 P 的抖动峰峰值是多少
峰峰值计算为 Nσ,其中 N 是波峰因数,确定需要包含多少高斯尾部才能产生误差概率 P。计算器在求解 N 的以下方程后计算此峰峰值,
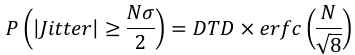
其中 DTD 是信号的数据传输密度,erfc 是互补误差函数。对于数据信号,DTD 定义为转换(或边沿)与位数的比率。对于时钟信号,设置DTD=1。
使用整数或科学记数法输入下面的数字(例如,将 123 输入为 123、1.23e2 或 1.23E2)。
RMS 到峰峰值抖动计算器
提供下表供快速参考。
| 概率(P) | 波峰因数 (N) | |
| DTD = 0.5 | 数据类型定义 = 1 | |
| 1e-1 | 2.563 | 3.290 |
| 1e-2 | 4.653 | 5.152 |
| 1e-3 | 6.180 | 6.581 |
| 1e-4 | 7.438 | 7.781 |
| 1e-5 | 8.530 | 8.834 |
| 1e-6 | 9.507 | 9.783 |
| 1e-7 | 10.399 | 10.653 |
| 1e-8 | 11.224 | 11.461 |
| 1e-9 | 11.996 | 12.219 |
| 1e-10 | 12.723 | 12.934 |
| 1e-11 | 13.412 | 13.613 |
| 1e-12 | 14.069 | 14.261 |
| 1e-13 | 14.698 | 14.882 |
| 1e-14 | 15.301 | 15.479 |
| 1e-15 | 15.883 | 16.054 |
| 1e-16 | 16.444 | 16.610 |