在实验室中,我们不需要知道系统的真实 BER。我们只需测量足够的数据即可确信 BER 低于某个指定水平。那么问题就变成了,如果我们重复传输 N 位,并检测到 E 错误,那么测得的 BER(即 E/N)将小于某个指定的 BER(例如 BER S )的测试百分比是多少?我们将此百分比称为 BER 置信度 (CL × 100%),并使用泊松分布计算如下。
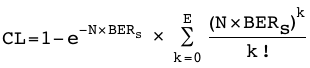
换句话说,CL × 100 是系统真实BER(即如果N = 无穷大)小于指定BER(例如BER S )的置信百分比。也就是说,如果重复测量无数次,测得的 BER 将小于(即优于)针对 CL × 100% 测试指定的 BER。
由于我们无法测量无限长的时间,因此 BER 置信水平始终低于 100%(至少理论上如此)。在开始 BER 测量之前,必须确定目标置信度。一些行业标准指定了这个水平(许多没有),95% 是一个合理的目标。所有行业标准都指定了最大系统 BER(我们在此称为 BER S )。
BER 测试:置信度计算器
使用下面的计算器,通过输入指定的 BER、数据速率、测量时间和检测到的错误数量来确定 BER 实验室测量的置信度。作为参考,传输位数 (N) 显示为数据速率 (BPS) 乘以测量时间 (T)。
或者,可以确定在实验室中必须测量多少位(即测量数据需要多少时间)才能达到特定的置信水平,假设一定数量的错误(通常为 0 个错误) — 只需输入 BER S 、BPS 和 E,然后更改 T 直到找到所需的置信水平。
以整数形式输入下面的数字,或使用科学记数法(例如,将 123 输入为 123、1.23e2 或 1.23E2)。
误码率测试示例
例如,必须传输多少位才能无错误地提供 95% 的置信水平,即真实 BER 小于 10 -12 ?在计算器中,输入 BER S = 1e-12、E = 0 和所需的 BPS。然后我们改变 T 直到置信水平达到 95%。这样,我们找到N = 3×10 12位(例如,当BPS = 10e9,并且T = 5 分钟时)。
这说明了一个有用的经验法则:测量 3÷BER S的比特数且没有错误,则满足指定 BER 的置信度为 95%。
解释此结果的另一种方法是,如果重复测量无数次,则 95% 的测试中测得的 BER 小于(即更好)指定的 BER。
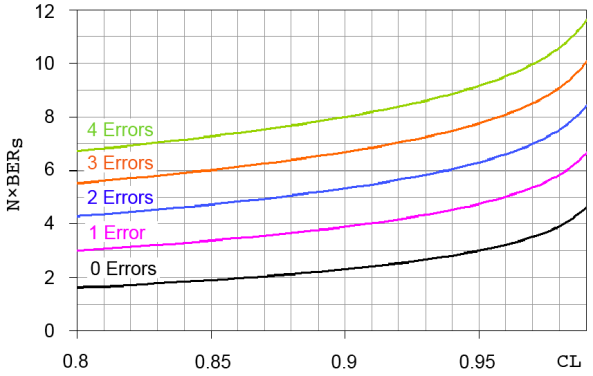
计算器用于生成下图。
该图有多种用途。如果要计算特定测量的 BER 置信水平,请将传输位数乘以指定的 BER,并在 Y 轴上的该点绘制一条水平线。找到与检测到的错误数量相对应的曲线,并在该曲线与刚刚绘制的水平线相交的地方画一条垂直线。测量的置信度是这条垂直线与 X 轴的交点。