RMS からピーク-ピーク ジッターへの計算 | 開発計算機に戻る
ランダム ノイズのみを含む信号を扱っており、そのジッター値が秒 RMS 単位でわかっています。この計算機の場合、データ信号に適用できるジッターのタイプはタイムインターバルエラー (TIE) です。クロック信号の場合、適用可能なジッタのタイプは何でも構いません (TIE、周期ジッタ、サイクル間ジッタなど)。いずれにしても、ジッター分布がガウス分布である場合、以下に示すように標準偏差 σ によって特徴付けられます。
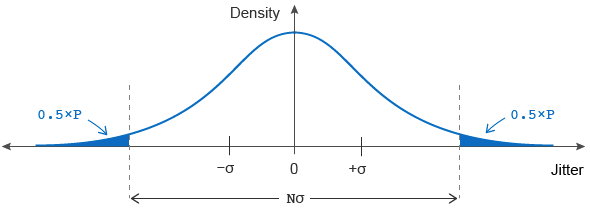
分布の平均はゼロであるため、その RMS 値は σ に等しいことに注意してください。分布の高さは、信号にその程度のジッターがある確率に関係します。
アプリケーションは、一定レベルの信頼性を持つように設計されています。これから、ジッターが大きくなりすぎるとシステムが故障する可能性がある確率 P の許容限界を導き出すことができます。グラフで見ると、この確率は、分布の総面積に対するパーセンテージとして上の図の実線の面積に等しくなります。たとえば、シックス シグマ設計 (例: σ=±3) は 99.73% の確率でエラーなしで実行されます (つまり P=0.0027、これは平均故障率 0.27% を表します)。
このエラーの確率 P に対するジッターのピーク-ピーク値が何であるかを知りたいとします。
ピーク-ピーク値は Nσ として計算されます。ここで、N は誤差 P を生成するためにどの程度のガウス テールを含める必要があるかを決定するクレスト ファクターです。計算機は、N について次の方程式を解いた後、このピーク-ピーク値を計算します。 、
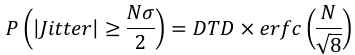
ここで、DTD は信号のデータ遷移密度、erfc は相補誤差関数です。データ信号の場合、DTD はビット数に対する遷移 (またはエッジ) の比率として定義されます。クロック信号の場合は、DTD=1 に設定してください。
整数または科学的表記法を使用して以下の数値を入力します (たとえば、123 を 123、1.23e2、または 1.23E2 と入力します)。
RMS からピーク-ピーク ジッターへの計算
次の表は、簡単に参照できるように提供されています。
| 確率(P) | クレストファクター(N) | |
| DTD = 0.5 | DTD = 1 | |
| 1e-1 | 2.563 | 3.290 |
| 1e-2 | 4.653 | 5.152 |
| 1e-3 | 6.180 | 6.581 |
| 1e-4 | 7.438 | 7.781 |
| 1e-5 | 8.530 | 8.834 |
| 1e-6 | 9.507 | 9.783 |
| 1e-7 | 10.399 | 10.653 |
| 1e-8 | 11.224 | 11.461 |
| 1e-9 | 11.996 | 12.219 |
| 1e-10 | 12.723 | 12.934 |
| 1e-11 | 13.412 | 13.613 |
| 1e-12 | 14.069 | 14.261 |
| 1e-13 | 14.698 | 14.882 |
| 1e-14 | 15.301 | 15.479 |
| 1e-15 | 15.883 | 16.054 |
| 1e-16 | 16.444 | 16.610 |